The Parabola Less Traveled

A parabola curved in a yellow wood,
And sorry I could not follow both
For be one traveler, long I stood
And looked up one as far as I could
As it approached infinite growth;

Then took the other, just as fair,
And having, perhaps, a negative claim,
Because it rose left, and wanted wear;
Though for each x the y-axis there
Had been worn really about the same

This parody joyfully brought forth from my mind, for in fifth grade I was made to memorize this poem, and have never forgotten it. For reference, this is Robert Frost (please see the link here).

If I could teach anything in the whole, wide world, it would be Mathematical History.

When their first word is, "AAAAAAH," something's going wrong.

No, not the the history of mathematics, where we would follow the evolution of the subject, holding all else constant--which, as it were, is the basis for most multi-variable equations.

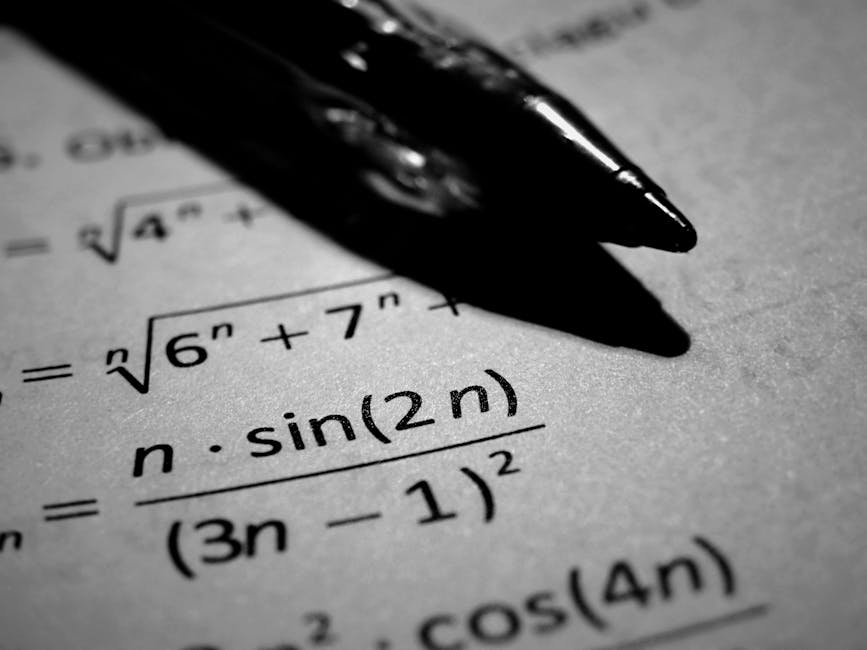I know that for the in focus on, n≠(1/3)...

I'm talking about using mathematics as the lens through which look through time and ask questions about the societies that we see.

We would start our journey with a little question and discussion: is math--or, maths if you're not from the USA--invented or discovered? I'm very much in the later category, that mathematics is the underpinning of the universe and not a mere figment of the human imagination. However, I'm really curious what the education system will have taught the kids so far, because I'm pretty sure that they've never been asked this question. Instead, they've probably been taught the subject by people who didn't get it (this is one of the big reasons why I hear a lot of people want to teach the younger grades. They just don't get multiplication and beyond, but that's a discussion for another day).

We would then go to ancient Greece. Why not Babylon? (You ask, if you know anything about the history of math). Because, I would reply, I don't want to get into a year long rant about how base 12 is so much better computationally than base 10, and if we really wanted to make a race of super humans they'd have six fingers on each hand, and how cool that would be, and it would just go on and on and on. No, we'd start in Ancient Greece. We would read texts about ratios, inequalities, logic, and geometry. We'd ask how their cosmology affected the questions these people asked, and what problems they used their mathematics to solve. My students would be beaten over the head with the fact that Pythagoras is not a person, but the PYTHAGOREANS were a group of people who may or may not have worshiped mathematics as a better way to understand perfection.

We would then follow the texts as they migrated through the Roman--later Byzantine--empire, and ask how their mathematical  principles affected their art and architecture. Next, would be the Muslim caliphates--centering on Baghdad--with comparing how their cosmology affected not only how they developed mathematics, but how they interpreted the earlier Greek work. We'd also ask to what extent their culture--being far more cosmopolitan and less xenophobic (the word, 'barbarian' literally comes from the word, 'bar', which is how the Greeks said that everyone else talked. Political correctness in any form was not their forte. Nor were woman's rights, abolitionism, wearing pants, etc.)--allowed them to grow the subject higher than the Greeks.

We'd end our journey through the empire with a brief trip through the Cordoba Caliphate--specifically a man named Averroes and the mathematical marvel that is the Alhambra--and then re-enter what would later be called Italy just in time for the Renaissance (assuming a two-semester class). We'd then go through the enlightenment, and end with a brief discussion unit on how the pocket calculator--and computerized number crunching in general--has changed both our view of mathematics and where/ how it can be applied.

Throughout this history, we'd follow several themes. The invented/ discovered discussion would obviously play a part, but we'd also be looking at how each culture used math. What were the problems they were trying to solve? Why weren't the current tools good enough? How did they make new ones? The goal is to show that math (and other subject..hint hint, cough cough, History, hint hint, cough cough) was studied in order to be used. People didn't find these formulas to be taught in class, but to solve a problem, an aspect that is sadly overlooked in too many subjects.

The last thread is what I'll call spontaneous development, which is where distant groups--such as, in this case, the Chinese in Asia, or the Maya in America--developed the same concepts and techniques. I do this because I personally feel that the more view points I can add into a discussion, the richer the discussion is. It also gives some of these groups--once again, the Maya--more agency than they have traditionally been given. These were not just people waiting in an idyllic paradise for the Europeans to come and introduce, "modernity." These were people who had problems and were active in trying to solve them, sometimes discovering ideas that Europeans and Muslims wouldn't know about for at least a century more. It also opens the door for some interesting questions: if they were using theories long before their counterparts across the ocean, then who really discovered it first? Likewise, in the micro, if two people in one culture discover something at roughly the same time (such as calculus) then who should get credit? Just some thoughts.

This has been another exciting adventure in the Austentatious. If you liked it, tell your friends; if you hated it, tell your enemies; and if you don't care either way, then tell everyone.